Tudo Quiz

Duas figuras planas, como os polígonos, são homólogas quando há correspondência ponto por ponto. Com relação a esse assunto, julgue o item abaixo.
Quando dois polígonos são semelhantes, o número que exprime a relação dos seus lados homólogos é denominado razão de semelhança.

Duas figuras planas, como os polígonos, são homólogas quando há correspondência ponto por ponto. Com relação a esse assunto, julgue o item abaixo.
Os polígonos semelhantes são polígonos transformados que apresentam um conjunto de características que tornam claras as suas relações com os polígonos que lhes deram origem.

Duas figuras planas, como os polígonos, são homólogas quando há correspondência ponto por ponto. Com relação a esse assunto, julgue o item abaixo.
Sabendo que segmentos homólogos são aqueles que unem pontos homólogos, as diagonais que unem vértices homólogos são corretamente denominadas diagonais homólogas.

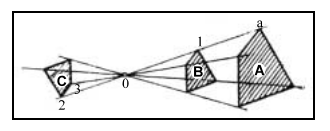
Quando dois polígonos são homotéticos, infere-se que eles são polígonos semelhantes colocados de maneira tal que seus lados homólogos fiquem paralelos. Polígonos ou figuras planas equivalentes apresentam uma mesma área, independentemente de suas formas. Considerando essas informações e a figura acima, julgue o item abaixo.
As figuras A e B são polígonos homotéticos.

Quando dois polígonos são homotéticos, infere-se que eles são polígonos semelhantes colocados de maneira tal que seus lados homólogos fiquem paralelos. Polígonos ou figuras planas equivalentes apresentam uma mesma área, independentemente de suas formas. Considerando essas informações e a figura acima, julgue o item abaixo.
É correto afirmar que a figura C possui homotetia indireta e as figuras B e A, direta.

Quando dois polígonos são homotéticos, infere-se que eles são polígonos semelhantes colocados de maneira tal que seus lados homólogos fiquem paralelos. Polígonos ou figuras planas equivalentes apresentam uma mesma área, independentemente de suas formas. Considerando essas informações e a figura acima, julgue o item abaixo.
O polígono A é equivalente ao polígono C.

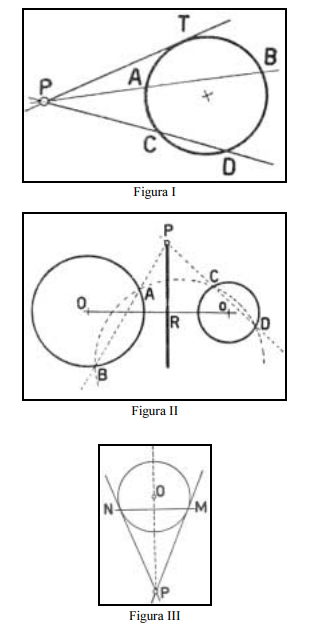
A potência de um ponto P em relação a um círculo é o produto das distâncias de P aos dois pontos de interceptação na circunferência da uma secante orientada que passa por P. Com base nessa afirmação e tomando como referência as figuras acima, julgue o item abaixo.
Na figura I, a potência ( p ) do ponto P, sendo a secante orientada PAB, tem como resultado p = PA × PB.

A potência de um ponto P em relação a um círculo é o produto das distâncias de P aos dois pontos de interceptação na circunferência da uma secante orientada que passa por P. Com base nessa afirmação e tomando como referência as figuras acima, julgue o item abaixo.
Se, na figura I, for definida uma outra secante orientada PCD, é correto afirmar que PA × PB = PC × PD.

A potência de um ponto P em relação a um círculo é o produto das distâncias de P aos dois pontos de interceptação na circunferência da uma secante orientada que passa por P. Com base nessa afirmação e tomando como referência as figuras acima, julgue o item abaixo.
Considere que o eixo radical de duas circunferências é definido como sendo o lugar geométrico dos pontos do plano que tem igual potência em relação a duas curvas. Partindo desse pressuposto, é correto afirmar que na figura II a reta PR é o eixo radical das circunferências.

A potência de um ponto P em relação a um círculo é o produto das distâncias de P aos dois pontos de interceptação na circunferência da uma secante orientada que passa por P. Com base nessa afirmação e tomando como referência as figuras acima, julgue o item abaixo.
O eixo radical é uma reta que pode ser inclinada em relação à reta suporte que une os centros de duas circunferências.